子供の考える力・書く力はこうすれば伸びる！

　中学生に数学を指導していると、解き方や計算以前に「題意をきちんと把握できない」生徒が登場します。特に図形の問題で、問題文に図が示されておらず「△ＡＢＣが円Ｏに内接しているとき……」といった条件をもとに自分で図を描く必要が生じるときにこの傾向は顕著です。我々の指導はすべて「初めて見た文章を正しく把握できている」ことが前提になっていますが、最近は問題を考える作業の前段階にあたる部分でつまずく子どもの存在を無視できなくなってきました。

題意を把握できない理由は読解力だけではない

　先ほどの「△ＡＢＣが円Ｏに内接しているとき……」という一文を読んで、自力で描いてほしい図はこのようになります。この円は△ＡＢＣの「外接円」とよばれるものですが、「△ＡＢＣ、円Ｏ、内接」というキーワードだけを見て△ＡＢＣの内側に円を描く（△ＡＢＣの内接円）生徒が多く、円が三角形の外側にあることを読み取れないのです

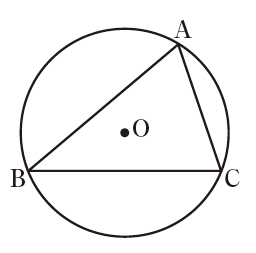
　一般に、我々大人が想像する読解力といえば「国語や英語の長文を読みこなして大意をつかむ能力」のことになりますが、決して少なくない子どもたちが課題として抱えているのは、これよりもっともっと前段階の「てにをは」の理解だったり、主語を把握することだったり、といった大人にとっては当たり前すぎて議論されることすらないことなのです。これを裏付ける資料として、先だって東京都の小中学生を対象に実施された「児童・生徒の学力向上を図るための調査」の結果をご紹介します。

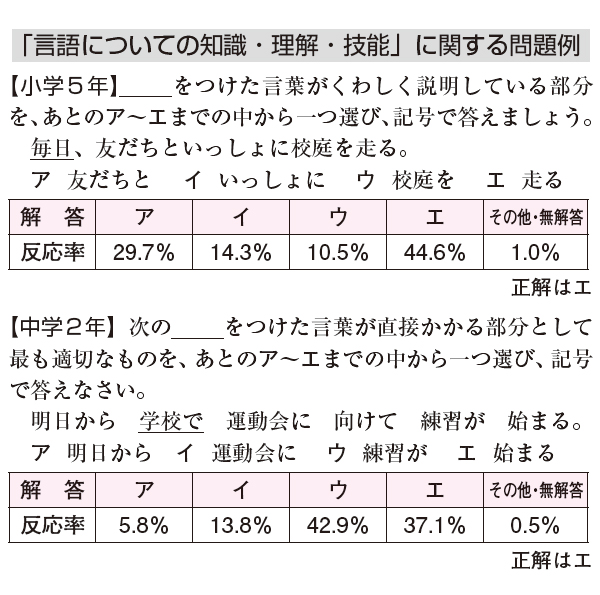
　小学５年では修飾と被修飾の関係、中学２年では語句の係り受けが問われていますが、半数以上の子どもたちが「毎日→走る」「学校で→始まる」と読めていないことに私は驚きました。
　学校で「教科書に書いてあるからちゃんと読んでおくように」と宿題が出たとすれば、求められているポイントがずれてしまう生徒がたくさん生じている可能性がありますし、自習なら問題集の解説の意味を読み取れないこともあるでしょう。最近流行の映像授業では、講師が話し言葉になる分だけ主語や述語があいまいになりますから、解説の意図を把握できずただ聞き流して終わってしまうことさえあるかもしれません。
　算数・数学では計算ドリルを丁寧に解き切ることで定着する土台部分も無視できませんが、それを超えて受験勉強に進む際には、正しく問題文を読み取る力も並行して鍛えておかなければなりません。これをおろそかにすれば、いくら勉強時間を長く確保しようともテストの結果には結びつかないのです。

新しい大学入試にも影響を及ぼす「数学と読解力」

　2021年春から新しく始まる大学入試共通テストでは、英語の民間試験のことばかりが話題になっていますが、数学でも「読解力」という点で大きな変化が生じる見込みです。従来型の数学の問題とは比較にならない分量の文章（会話文もある）を読み、解答するために必要な条件を拾いながら図を描き情報をまとめ、最後に処理を行って解答を導くようになりますので、制限時間が長くなるとはいえ受験生にとってより難しいと感じるテストになりそうです。昨年秋に実施された試行調査の概要（下表）をご覧ください。

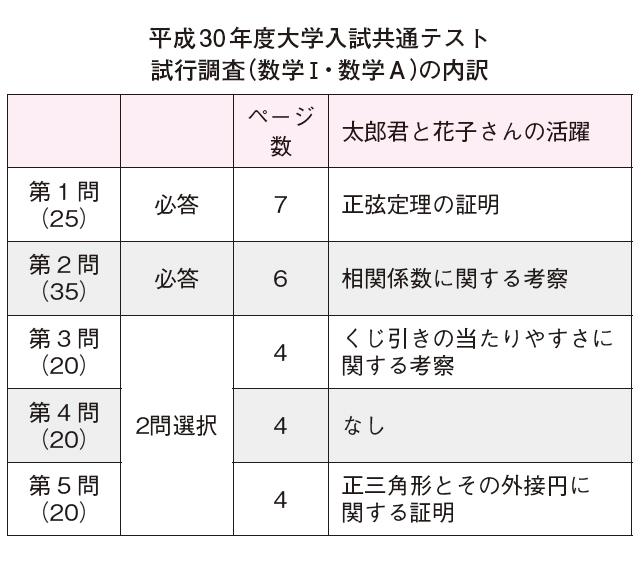
　注目すべきは「太郎君と花子さんの活躍」です。全５問中４問で太郎君と花子さんが登場し、正弦定理という公式の成り立ちをそれぞれ証明してみたり、箱に入ったくじを引く際の当たりやすさについて検証したり、といった“活躍”を見せ、受験生は二人の会話の内容を読み取った上で解答しなくてはなりません。「知識やテクニック、公式を暗記していれば解けるだろう」という甘い認識では通用しません。
　70分という制限時間の中でこれほどの量を処理するには
・太郎君と花子さんの会話を自分の学習した内容と結びつける練習
・会話の概要を１回で把握する練習（何度も読み直す時間がない）
をしておく必要があります。冒頭で紹介した「△ＡＢＣが円Ｏに内接しているとき……」という一文は、普段の勉強では「△ＡＢＣの外接円をＯとする」と表現されていることです。このような「問題文の表現を自分が経験したパターンに置き換える」作業は、小学生の段階から日常生活の中でしっかりと意識し、早くから取り組んでおくことが大切です。
　「ドリルと同じ文章で数字が違うだけなら解けるけれど、ちょっと設定が面倒になったり答えるものが変わると戸惑ったりする」という傾向には注意を払い、いきなり計算式を書くのではなく図や絵あるいは表を用いて情報を整理させるといいでしょう。「そんなことをしなくても簡単だから大丈夫！」と子どもはほぼ100％言いますが、後のことを考えると間違いなく大丈夫ではありません。
　また、概要を１回で把握する練習については、普段の勉強において「公式は知っているけれど証明はできない」「テクニックは知っているけれど、それを使えば解ける理由はわからない」という状態を減らす努力を繰り返すしかありません。速さを学ぶ際に多くの子どもが指導される「は・じ・き（み・は・じ）」の公式であったり、単位の換算では便利な道具を用いたり、中学入試を志す子どもでは「流水算のパターン」「旅人算のときはこの解き方」「三角形の面積比で使えるテクニック」といった数えきれないほど紹介される解法であったりと該当する事例は様々ですが、せめて友だちや家族の皆さんにはこれらが使える理由を説明できることを目指したいところです。「（理由はわからないけれど）丸暗記する→時が経つと忘れる」の繰り返しで中途半端な状態のまま放置されている場合、「覚えるまで何度でも繰り返す」ことが根本的解決にならないことを気に留めておきましょう。

平成31年度「児童・生徒の学力向上を図るための調査」東京都教育委員会

vol.140　ブンブンどりむ　保護者向け情報誌「ぱぁとなぁ」2019年12月号掲載