子供の考える力・書く力はこうすれば伸びる！

　いきなりですが、みなさまは「素数」とはどんな数のことか説明できますか？現行の指導要領では小５で初めて登場し、中１で「素因数分解」を学習する際に定着させる流れになっています。ところが、先日実施された全国学力調査によると、中学3年生で正しく「素数」を理解している生徒が３人に１人（正答率は32.2％）しかいないことがわかりました。小学生保護者にとっても中学生保護者にとっても他人事では済まされない実情について詳しくみていきましょう。

小５・中１で登場する「素数」に苦戦する中３生

　まずは、令和７年度（2025年度）「全国学力・学習状況調査」で出題された数学（中３生向け）の問題【資料１】をご覧ください。
　素数とは、中学校の教科書に沿って説明すると「１より大きい自然数で、１とその数自身しか約数を持たない数…①」となります。本問では２、３、５、７の４つの数を選べば正解ですが、誤答の要因は「１は素数なのか、素数じゃないのか」を理解できていない点にあることは、みなさまも予想できることでしょう。もしもお子さまが素数について迷っていたとしたら、みなさまはどのように説明しますか。
　現行の中１教科書では、①の説明は掲載されているものの「なぜ１は素数ではないのか」について言及はありません。佐賀県が公表している分析結果では、指導改善策として
　・「なぜ１は素数ではないのか」を生徒なりに考える場面を設定する。
　・その後の学習において素数を用いる際に、１は素数に含まれないことを再確認するような場面を意図的に設定する。
とありますが、中３生の３人に２人が素数について正しく理解できていない現状の中で、ヒントや誘導もなく「なぜ１は素数じゃないのか、みんなで考えよう！」と中１で授業を用意しても、塾や動画で知識を得ている生徒以外は議論に参加することが難しいと想像できます。
　我々保護者世代が子どもの頃は、①を覚えてしまえば事足りました。素数に１が入るのか入らないのか、それは「①をしっかり覚えていればわかる、教科書に正解が書いてある」で説明が終わっていたのです。しかし現在は、このスタイルでは子どもたちが消化不良を起こしていることがハッキリと数値で見て取れます。もしもお子さまから質問されたら、保護者自身も私も「なるほど」と理解してもらえる説明を提示してあげる必要があるのです。
　私は、①と合わせて「素数とは、（正の）約数が2つの数」と生徒たちに伝えます。たとえば10は1、2、5、10と4つの約数を持っているので素数ではありません。1は1×1としか表せないので約数は1つしかありません。よって、素数ではないのです。ちなみに、約数の求め方は小5で学習していますから、もしも中1生で「約数の求め方」を忘れているようであれば、大至急復習が必要になります。

「コブ」がない得点分布図を見たことがありますか？

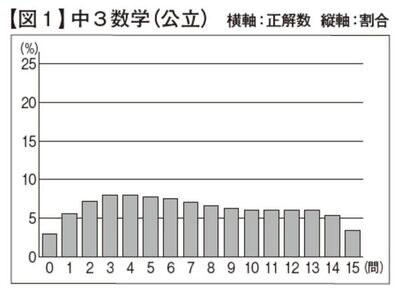
　毎年行われている「全国学力・学習状況調査」では、【資料１】に代表されるような「象徴的な問題」や平均点の推移（学力が向上した／低下した）が報道されますが、ここでは我々保護者世代と現在との決定的な差である「得点分布」に注目します。まずは【図１】をご覧ください。
　令和７年度（2025年度）「全国学力・学習状況調査」の中３数学では、公立中学生（89万人）の平均正答率が48.8％、中央値（ちょうど真ん中の生徒）の正解数が7.0問と公表されています。
　【図１】の得点分布状況で「データが集中していない」ことにご注目ください。平均値の周辺にデータが集中してラクダのコブのような形状になる分布図（正規分布）との違いは一目瞭然です。
　私が記憶している限り、2000年代くらいから様々なテスト結果において分布が二極化（ラクダのコブが上位層、下位層で２つできる）傾向がみられるようになりました。平均点付近にくぼみができるような形状が特徴で、この傾向を踏まえて公立中学でも英語や数学では２レベルの習熟度別授業を行うところが増えました。
　ところが【図１】ではコブがなくなっているのです。また、最も割合の高い層が正答数３問、４問といった平均以下であることにもご注目ください。公立中学生の数学理解度にこれだけバラつきがあると、先生は日々の授業構成にも苦労するはずです。どの層の生徒に合わせて授業を行えばよいのか、その目安がまったく見えてこないからです。我々保護者の側から見れば「学校の授業レベルと子どもの学力がちょうど合う」ことを期待できないことを意味します。授業や宿題のレベルをどこに合わせているのかしっかり把握し、過不足があればご家庭で調整しなければならないことを意味します。
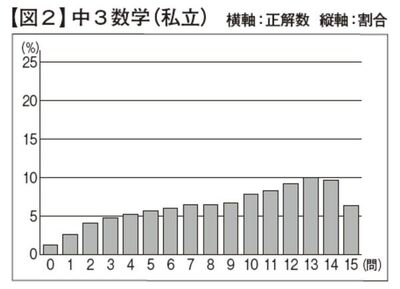
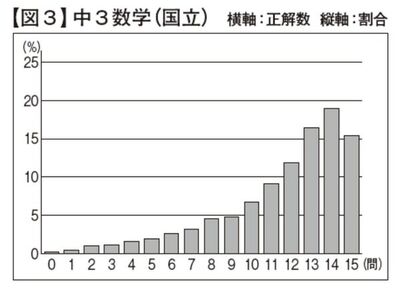
　参考として【図２】では私立中学生のデータ（1.65万人）、【図３】では国立中学生のデータ（0.9万人）の分布図もご紹介します。私立中学生は平均正答率が60.3％、中央値の正解数が10.0問ですが、分布図を見る限り私立中だからといって数学ができる生徒ばかりではないことが読み取れます。思っていたよりもコブが小さく平均正答数以下の生徒が多い印象を受けますが、学校ごとの差が大きいこともうかがえます。国立中学生は平均正答率が77.3％、中央値の正解数が13.0問と高くなっており、分布図でも正答数14問をピークとして大きなコブができています。これだと先生方は授業構成や到達度のイメージがしやすいことでしょう。

見るべきは「優劣」ではなく「個別最適化」

　【図１】～【図３】の分布図を見れば、公立・私立・国立の中学校別の状況に差があることは明らかです。また、平均正答率・正答数の詳細は都道府県レベル、市町村レベル、教育委員会レベルで公表されていますから、自治体別の比較も可能です。しかしながら、この分布図を見る限り、報道やＳＮＳあるいは学校現場が「優劣」を論じたりこだわったりしている場合ではない、と私は強く思います。隣の自治体よりも平均が高かった、国立中学はできがいいけれど公立中は、なんて話題よりも「コブがない分布図の衝撃」のほうが何倍も重要で、数学あるいは算数との向き合い方を先生も保護者も生徒個々に合わせて考えてあげる必要性をデータがハッキリと示しています。
　数学や算数を勉強する目的は、けっして「よい高校やよい大学に合格するため」ではありません。中学生までの間は、社会に出たときに必要とされる「経験を基にして自分で考える習慣」を身に付けるためのツールでしかなく、素数の意味もわからずに素因数分解を練習したところで、成り立ちの意味が説明できない解き方や公式をただ丸暗記することで得た点数からは「20年後につながるものはない」ということは、我々大人が一番わかっているはずですから。

参考資料：令和7年度 全国学力・学習状況調査 調査結果資料【全国版/中学校】国立教育政策研究所

vol.210　ブンブンどりむ　保護者向け情報誌「ぱぁとなぁ」2025年10月号掲載